图
tip
部分可见 此。
握手定理
无向图每条边提供 2 个度。
任何图(无向图、有向图)中,度数为奇数的顶点个数一定是偶数。
生成子图
顶点一致,边不一样。
补图
补的是边,补完可以凑成一个完全图,补图就是原来的节点和所补的边构成的图。
通路/回路
所有边都不相同是简单通路/回路;
所有顶点都不相同是是初级通路/回路。
有边重复出现是复杂通路/回路。
n 阶图中两顶点存在通路,则这两点之间一定存在一个长度小于 的通路。
邻接矩阵的乘
x 次方就表示两点之间长度为 x 的路径有多少条
回路就是对角线之和。
可达性矩阵
求出邻接矩阵的 次方,并取并集。
通过可达性矩阵与其转置乘积,可以得到两个节点直接是否是相互连通的。再通过矩阵初等变换,得到强连通分图:
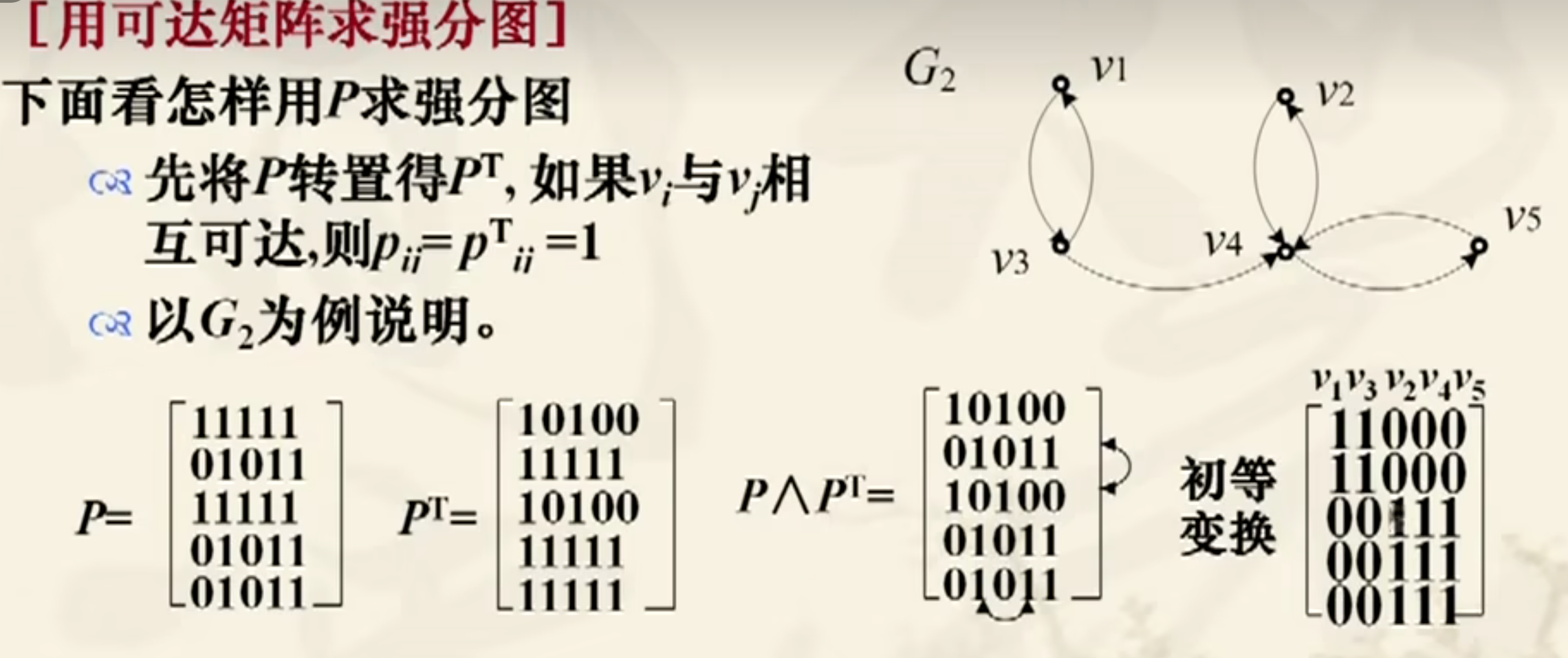
其中 和 是强连通分图。
Wallshall 算法
关联矩阵
表示顶点和边是否关联,因此每列只有两个 1,每行 1 的个数是节点的度数。
有向图则使用 -1,1,0 表示,因此每列有一个 1 和一个 -1。
欧拉图
欧拉通路/回路,经过图中每条边一次且近有一次的通路/通��路。
有欧拉回路的图就是欧拉图。
有欧拉通路而无欧拉回路的图是 半欧拉图。
tip
无向图是欧拉图当且仅当图连通且无 奇度数顶点
无向图是半欧拉图当且仅当图连通且 恰有两个奇度数顶点
有向图是欧拉图当且仅当图是强连通的且 每个顶点的出入度相同
有向图是半欧拉图当且仅当图是单向连通且 恰有两个奇度数顶点,其中一个入度比出度大一,另一个出度比入度大一,其他顶点出入度相同
有向图是非平凡的欧拉图当且仅当图是连通的且为若干个边不重的圈之并,可以用于构造欧拉回路
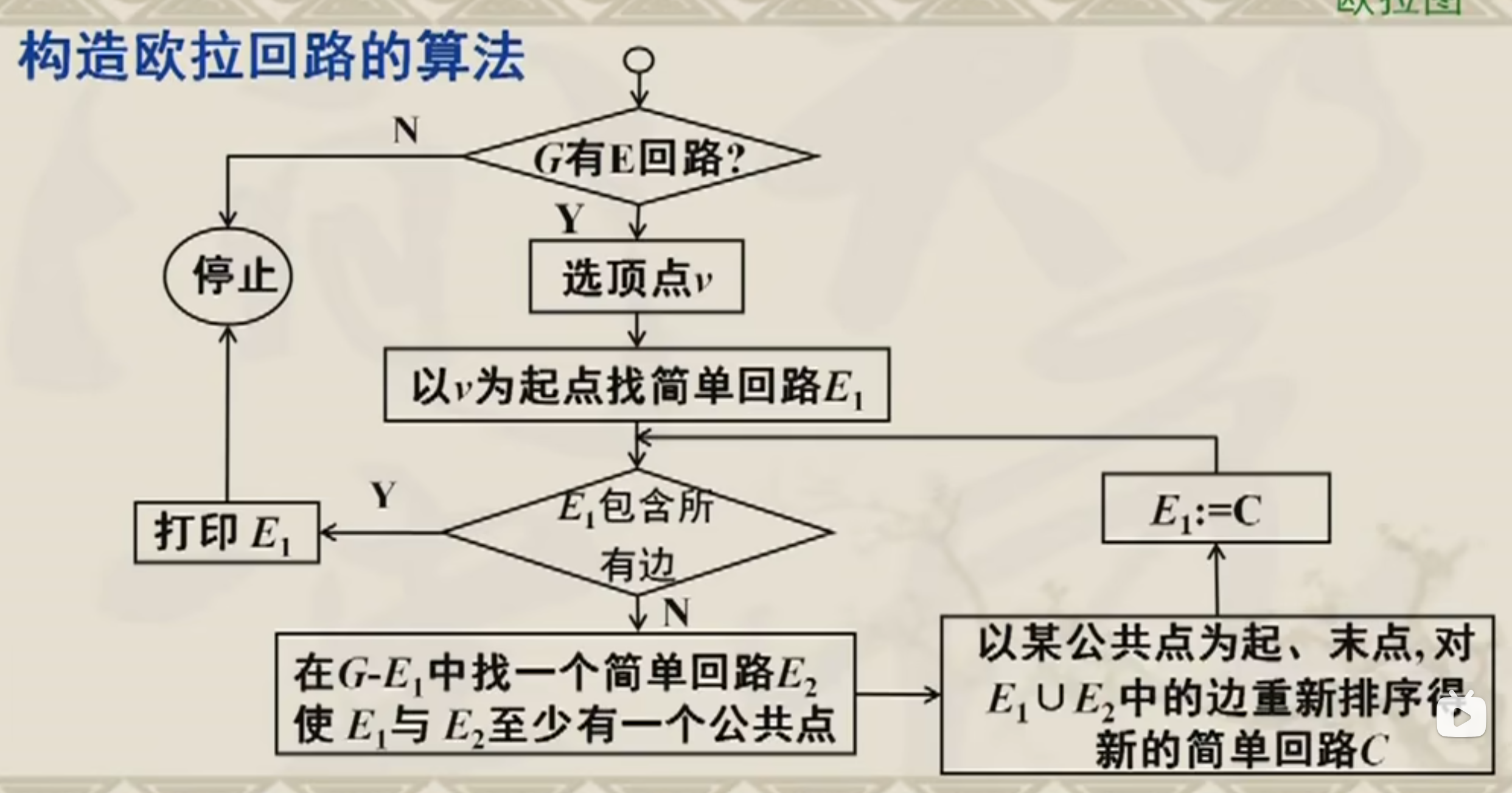
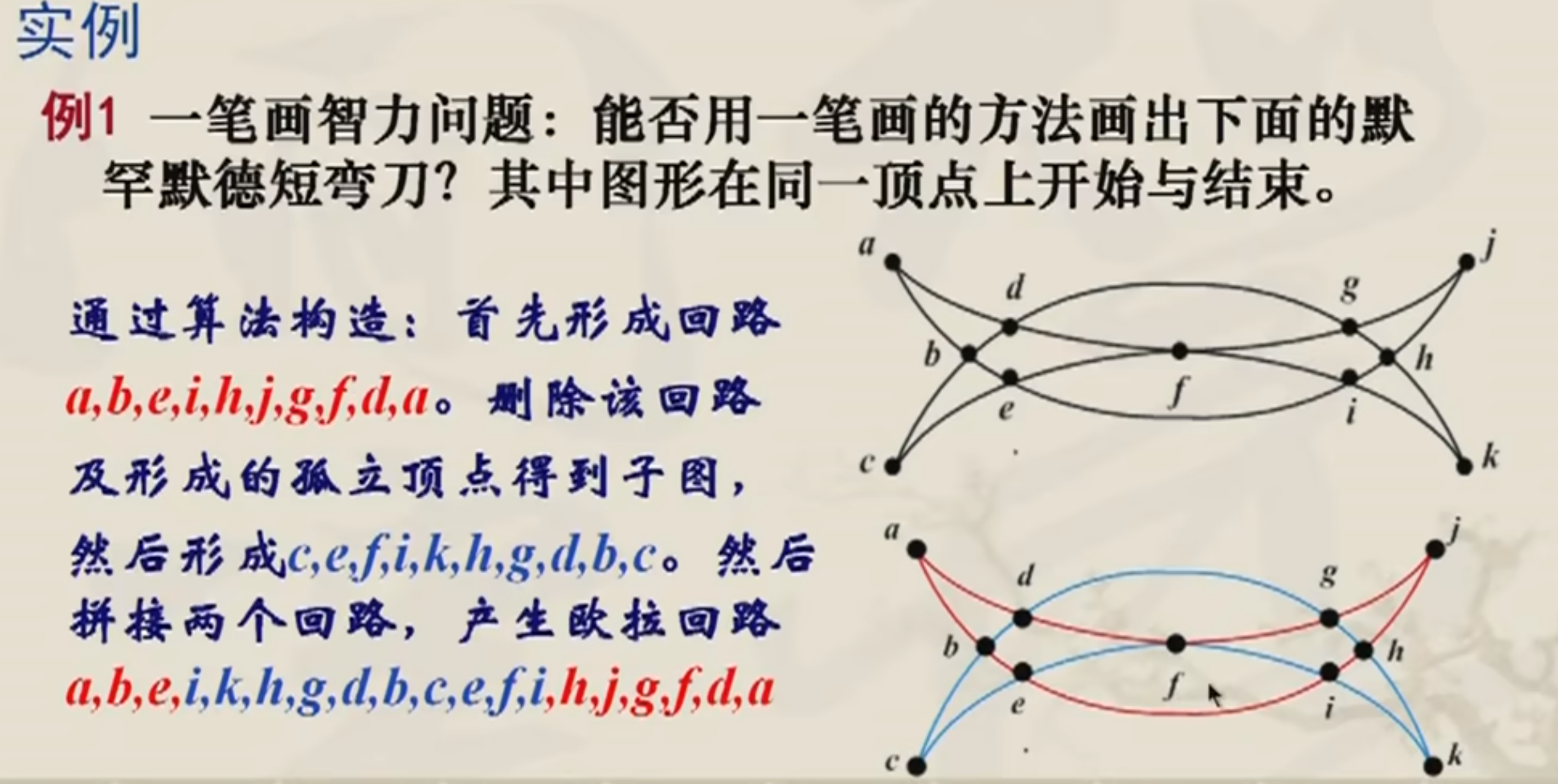
哈密尔顿图
将欧拉回路/通路的条件换成顶点,即经过图中每个顶点一次且近有一次的通路/通路。
info
平凡图是哈密尔顿图,平行边和环不影响哈密尔顿性;其实质是将所有顶点排在一个圈上。