Transformer：Attention Is All You Need

论文名称：Attention Is All you Need

作者：Ashish Vaswani，Noam Shazeer，Niki Parmar，Jakob Uszkoreit，Llion Jones，Aidan N. Gomez，Łukasz Kaiser，Illia Polosukhin

code：https://github.com/jadore801120/attention-is-all-you-need-pytorch

前言

基于 RNN 或 CNN 的 Encoder-Decoder 模型在 NLP 领域占据大壁江山，然而她们也并非是完美无缺的：

LSTM，GRU 等 RNN 模型受限于固有的循环顺序结构，无法实现并行计算，在序列较长时，计算效率尤其低下，虽然最近的工作如因子分解技巧 ¹，条件计算 ²在一定程度上提高了计算效率和性能，但是顺序计算的限制依然存在；
Extended Neural GPU³, ByteNet ⁴,和 ConvS2S ⁵ 等 CNN 模型虽然可以进行并行计算，但是学习任意两个位置的信号的长距离关系依旧比较困难，其计算复杂度随距离线性或对数增长。

而谷歌选择抛弃了主流模型固有的结构，提出了完全基于注意力机制的 Transformer，拥有其他模型无法比拟的优势：

Transformer 可以高效的并行训练，因此速度十分快，在8个 GPU 上训练了3.5天；
对于长距离关系的学习，Transformer 将时间复杂度降低到了常数，并且使用多头注意力来抵消位置信息的平均加权造成的有效分辨率降低
Transform 是一种自编码（Auto-Encoding）模型，能够同时利用上下文

整体结构

Transformer 的整体结构是一个 Encoder-Decoder，自编码模型主要应用于语意理解，对于生成任务还是自回归模型更有优势

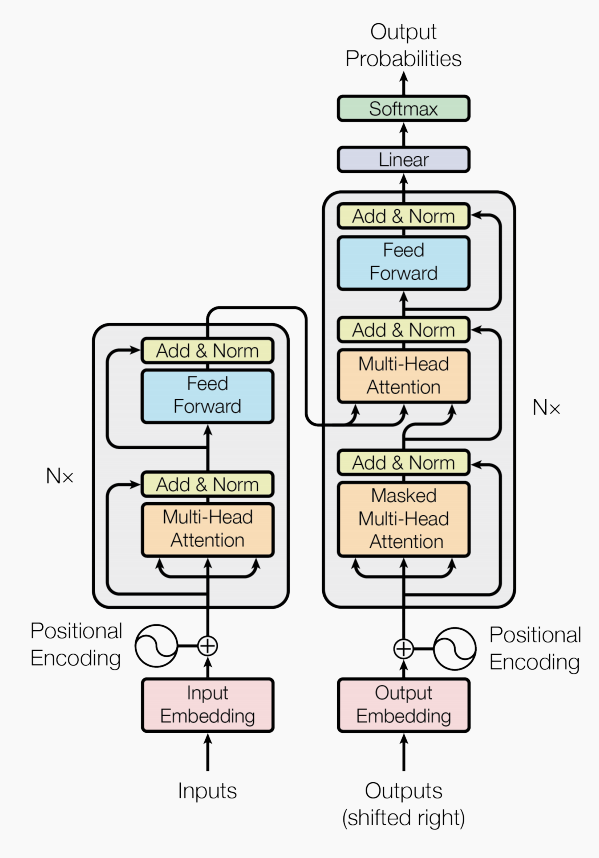
我们可以将其分为四个部分：输入，编码块，解码块与输出

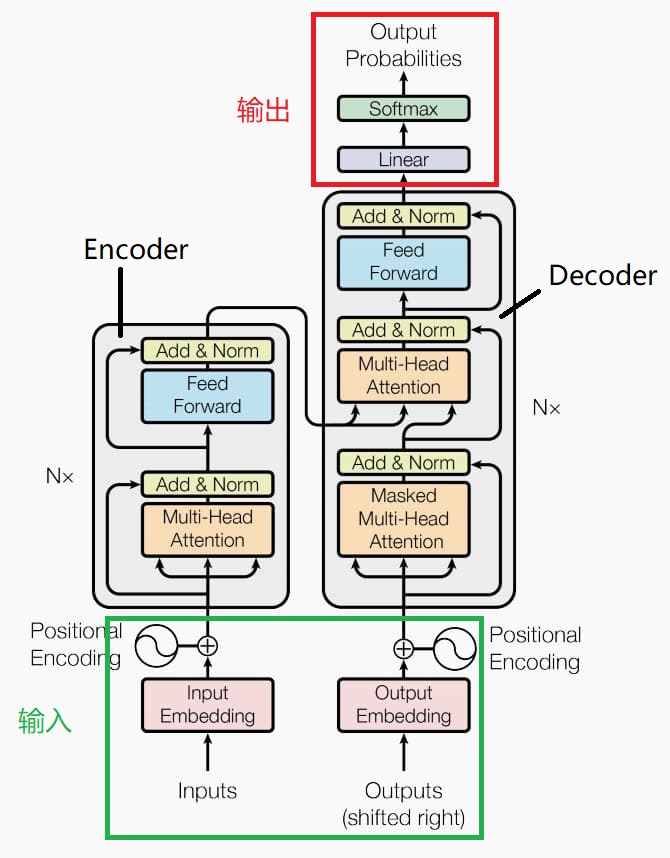
接下来让我们按照顺序来了解整个结构，希望在阅读下文前你可以仔细观察这幅图，阅读时也请参考该图

输入

使用 nn.Embedding 进行 Word Embedding，论文中嵌入维度 $d_{model}=512$

在嵌入时，左右两部分的权重会共享

得到词嵌入向量后需要乘以 $\sqrt{d_{model}}$ ，其原因可能是为了相对减小位置编码的影响

同时会将上一层的输出加入进来，网络的第一层则会直接使用 Inputs 充当“上一层”

在输入之后会进行位置编码，使得 Transformer 拥有捕捉序列顺序的能力

Encoder-Decoder

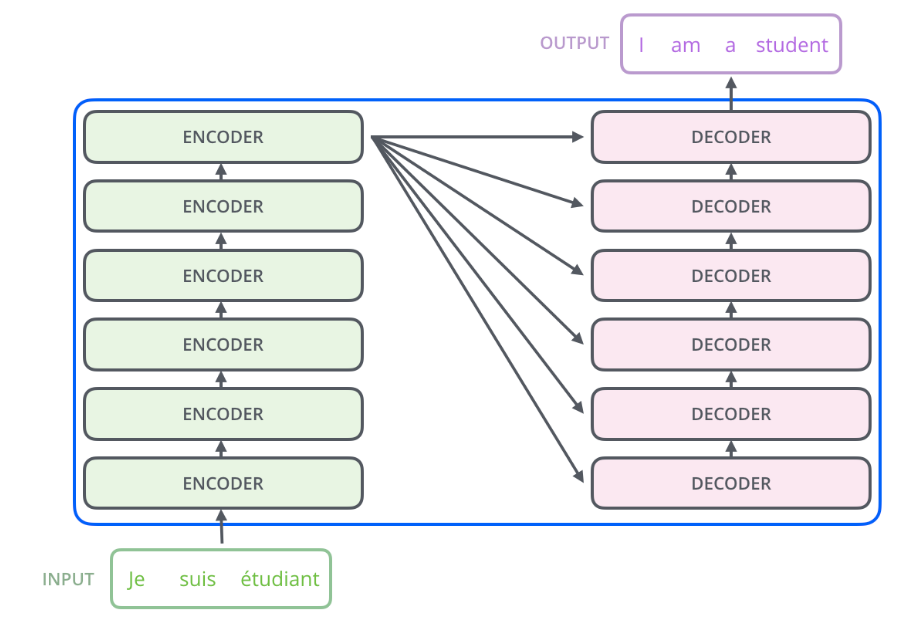
整体结构如图

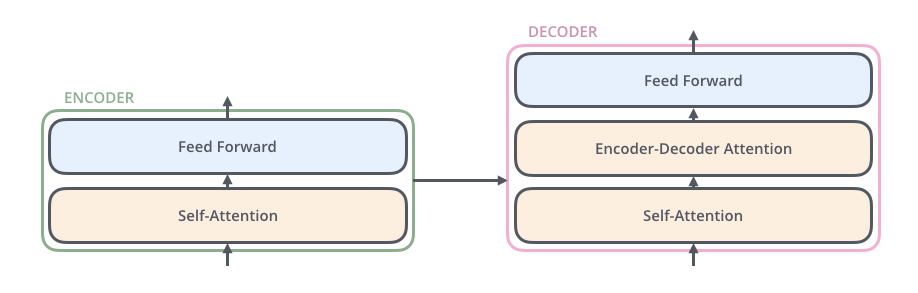
Encoder-Decoder 的内部结构如下图：

Encoder：编码块是由6个完全相同的 layer 组成的，每个 layer 有两个子层

第一层包括一个 $Multi\ Head\ Self-Attention$ 、 $Layer\ Normalization$ 和残差连接

第二层包括一个二层的全连接前馈层： $FFN(x)=max(0,xW_1+b_1)W_2+b_2$ ,中间层的维度为2048；同样包含 $Layer\ Normalization$ 和残差连接
Decoder：解码块同样由6个完全相同的 layer 组成，每个子层同样有残差连接和 $Layer\ Normalization$

额外添加了第三个子层—— $Masked\ Multi\ Head \ Attention$ ，这是针对于上一层输出的，将在下文详细解读

此外，还修改了子注意力子层（如上图，由原来的 Self-Attention 变 Encoder-Decoder Attention）

Layer Normalization：NLP 任务中主要使用 $Layer\ Norm$ 而不是 $Batch\ Norm$ ，因为在批次上进行归一化会混乱不同语句之间的信息，我们需要在每个语句之中进行归一化。

输出

对解码器的输出使用普通的线性变化与 $Softmax$ ，作为下一层的输入

注意力机制

Self-Attention

具体内容可参考我的另一篇博客——注意力机制

缩放点积注意力

缩放点积注意力，图式如下：

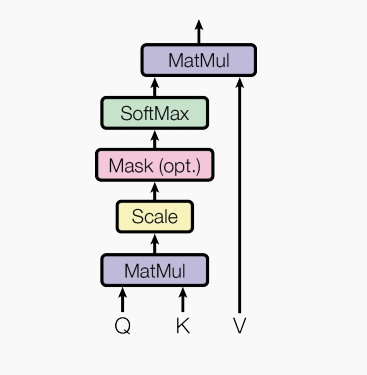
其公式为

Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V

缩放点积指的是其中的打分函数

\frac{QK^T}{\sqrt d}

常见的注意力模型有加性模型和点积模型，点积模型相较于加性模型效率更高，但是当输入向量维度过高，点积模型通常有较大的方差，从而导致softmax函数梯度很小，而缩放点积模型可以很好地解决这个问题。

另为，Transformer 在实现过程中使用了残差连接

Softmax梯度问题：

S_i=\frac{e^{x_i}}{\sum_{j=1}^Ne^{x_j}}

我们知道， $Softmax$ 的作用是拉大数据之间的差距

对于一组数据 $[x,x,2x]$ ，让我们给其赋不同的值，来观察方差和 $S_3$ 的变化

import numpy as np
x = np.array([np.exp([i, i, 2*i]) for i in [1, 10, 100]])
print(np.square(np.linalg.norm(x, axis=1, ord=2)))  # 方差S
print(x[:, 2]/x.sum(axis=1).T) # S3

\begin{cases}{} x=1\quad S=6.938\quad S_3=0.576 \\ x=10 \quad S=2.253e17\quad S_3=0.999\\ x=100\quad S=5.221e173\quad S_3=1.0 \end{cases}

即使数据之间成比例，在数量级较大时，Softmax将几乎全部的概率分布都分配给了最大的那个数

Softmax 的梯度为

\frac{\partial S(x)}{\partial x}= \left[\begin{array} {c}y_1&0&\cdots&0\\ 0&y_2&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&y_d \end{array}\right]- \left[\begin{array} {} y_1^2&y_1y_2&\cdots&y_1y_d\\ y_2y_1&y_2^2&\cdots&y_2y_d\\ \vdots&\vdots&\ddots&\vdots\\ y_dy_1&y_dy_2&\cdots&y_d^2 \end{array}\right]

当出现上述的情况时，softmax 会输出一个近似 one-hot 的向量 $[1,0,0,\cdots,0]$ ,此时梯度为

\frac{\partial S(x)}{\partial x}= \left[\begin{array} {c}1&0&\cdots&0\\ 0&0&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&0 \end{array}\right]- \left[\begin{array} {} 1^2&0&\cdots&0\\ 0&0&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&0 \end{array}\right]=0

缩放点积为什么有效？

在论文的注脚中给出了如下假设：

**假设向量 $Q$ 和 $K$ 的各个分量是互相独立的随机变量，均值是0，方差是1，那么点积 $QK$ 的均值是0，方差是 $d_k$ **

具体推理过程可参考我的另一篇博客概率论 2.3.5和2.3.6节

我们在高二就学过方差的一个基本性质，对于随机变量 $Y=aX+b$

\sigma_Y^2=a^2\sigma_X^2

所以除以 $\sqrt{d_k}$ 可以将方差控制为1，从而有效地解决梯度消失的情况

Multi-Head Attention

多头注意力，图式如下

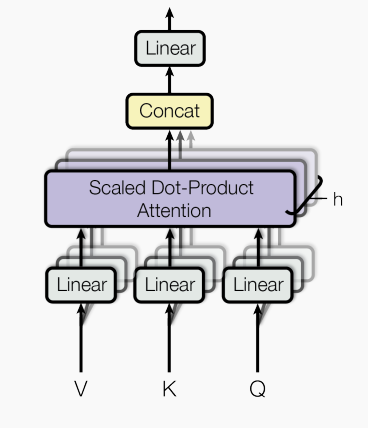
相比于使用 $d_{model}$ 维数（此处为512维）的 $Q、K、V$ 来执行一个 $Attention$ ，使用不同的线性映射得到多个 $Q、K、V$ 来并行得执行 $Attention$ 效果更佳，原因如下：

其增强了模型专注于不同信息的能力
为注意力层提供了多个“表示子空间”

具体操作：

对于每一个头，我们使用一套单独的权重矩阵 $W_Q、W_K、W_V$ ，并且将其维度降至 $d_{model}/H$

生成 H 个不同的注意力矩阵，将其拼接在一起

最后使用一个单独的权重矩阵 $W^O$ 得到最终的注意力权重

MutiHead(Q,K,V)=Concat(head_1,head_2,\cdots,head_h)W^O\\where\quad head_i=Attention(QW^Q_i,KW^K_i,VW^V_i)

由于维度做了缩放，多头注意力的总代价和仅使用一个注意力的代价相近

与卷积的关系：

我们可以发现，多头注意力实际上与卷积有着异曲同工之妙

正如多个头可以注意不同的信息，不同的卷积核可以提取图像中不同的特征

同样，正如特征图多个通道内的信息冗余，多头注意力也存在着信息冗余

位置编码

主要参考

为什么需要位置编码？

上文已经提到，Transformer 是一种并行计算，为了让模型能够捕捉到序列的顺序关系，引入了位置编码，来获得单词之间的相对距离。

正余弦位置编码

PE(pos,2i) = \sin(\frac{pos}{10000^{\frac{2i}{d_{model}}}})\\ PE(pos,2i+1) = \cos(\frac{pos}{10000^{\frac{2i}{d_{model}}}})\\

对于奇数位置使用余弦函数进行编码

对于偶数位置使用正弦函数进行编码

注意：这里的位置指的是一个词向量里数据的位置，pos 指的才是单词在语句中的位置

例如某个单词在语句中的位置为 Pos=5， $d_{model}=512$ ，则其位置编码向量为

\left[\begin{array}{c}sin(\frac{5}{10000^{\frac{0}{512}}})\\cos(\frac{5}{10000^{\frac{0}{512}}})\\sin(\frac{5}{10000^{\frac{2}{512}}})\\cos(\frac{5}{10000^{\frac{2}{512}}})\\\vdots\\sin(\frac{5}{10000^{\frac{512}{512}}})\end{array}\right]

可以看到， $2i、2i+1$ 仅仅决定使用的是 $sin$ 还是 $cos$ ，对于同一个 $i$ ，内部是相同的

得到位置编码之后，将其与词向量相加，作为最终的输入

这里的直觉是，将位置编码添加到词向量，它们投影到 $Q/K/V$ 并且进行点积时，会提供有意义的距离信息

为什么位置编码是有效的？

我们在小学二年级就学过三角函数的诱导公式：

\sin(\alpha+\beta)=sin(\alpha)cos(\beta)+cos(\alpha)sin(\beta)\\ cos(\alpha+\beta)=cos(\alpha)cos(\beta)-sin(\alpha)sin(\beta)

可以得到：

PE(pos+k,2i)=PE(pos,2i)PE(k,2i+1)+PE(pos,2i+1)PE(k,2i)\\ PE(pos+k,2i+1)=PE(pos,2i+1)PE(k,2i+1)-PE(pos,2i)PE(k,2i)

我们令 $u(k)=PE(k,2i)、v(k)=PE(k,2i+1)$ ，得：

\left[\begin{array} {c}PE(pos+k,2i)\\ PE(pos+k,2i+1) \end{array} \right]= \left[\begin{array} {c}v(k)&u(k)\\-u(k)&v(k) \end{array} \right] \left[\begin{array} {c}PE(pos,2i)\\PE(pos,2i+1) \end{array}\right]

给定相对距离 $k$ ， $PE(pos+k)$ 与 $PE(pos)$ 之间具有线性关系

因此模型可以通过绝对位置的编码来更好地捕捉单词的相对位置关系

毫无疑问，位置编码在整个 Transformer 中的作用是巨大的

没有位置编码的 Tranformer 就是一个巨型词袋

接下来让我们看看正余弦位置编码的局限

相对距离的方向性

我们知道，点积可以表示相对距离，注意力机制中就使用点积作为打分函数来获取 $Q、K$ 的相似度，让我们看看两个相对距离为 k 的位置编码的距离

对于 $PE_{pos}$ ，令 $c_i=\frac{1}{10000^{\frac{2i}{d}}}$ ：

\begin{align} PE_{pos}&= \left[\begin{array} {c}PE(pos,0)\\PE(pos,1)\\PE(pos,2)\\ \vdots\\PE(pos,d) \end{array}\right]\\ &= \left[\begin{array} {c}sin(c_0pos)\\cos(c_0pos)\\sin(c_1pos)\\\vdots\\cos(c_{\frac{d}{2}-1}pos) \end{array}\right] \end{align}

内积可得：

\begin{align}PE_{pos}^TPE_{pos+k}&= \sum_{i=0}^{\frac{d}{2}-1}{sin(c_ipos)sin(c_i(pos+k))+cos(c_ipos)cos(c_i(pos+k))}\\ &=\sum_{i=0}^{\frac{d}{2}-1} {cos(c_i(pos+k-pos))}\\ &=\sum_{i=0}^{\frac{d}{2}-1}cos(c_ik) \end{align}

而余弦函数是一个偶函数，因此正余弦位置编码仅能捕捉到两单词之间的距离关系，而无法判断其位置关系

自注意力对位置编码的影响

在 Transformer 中，位置编码之后会进行自注意力的计算，公式如下：

score(x_i)=\frac{(x_iW_Q)(x_iW_K)^T}{\sqrt{d}}=\frac{((x_i^{position}+x_i^{word})W_Q)((x_i^{position}+x_i^{word})W_K)^T}{\sqrt{d}}

可以看到，经过自注意力的计算，模型实际上是无法保留单词之间的位置信息

那么 Transformer 是如何 work 的呢？

题外话：在 bert 中直接使用了 Learned Position Embedding 而非 Sinusoidal position encoding

解码块

Masked Multi-Head Attention

在机器翻译中，解码过程是一个顺序操作的过程，也就是当解码第 $k$ 个特征向量时，我们只能看到第 $k-1$ 及其之前的解码结果，因此使用了添加了 Mask，将当前词之后的词全都盖住

Endcoder-Decoder Attention

设计了一种解码块与编码块的交互模式

编码块最终的输入会生成不同的 $K，V$ （在代码中是这样体现的），输入给所有的解码器，而 $Q$ 则是来自于 Masked Multi-Head Attention

代码讲解

位置编码

class PositionalEncoding(nn.Module):

    def __init__(self, d_hid, n_position=200):
        super(PositionalEncoding, self).__init__()

        # Not a parameter
        # 在内存中定义一个名为pos_table的常量，可以通过self.pos_table使用，模型保存和加载的时候可以写入和读出。
        self.register_buffer(
            'pos_table', self._get_sinusoid_encoding_table(n_position, d_hid))

    def _get_sinusoid_encoding_table(self, n_position, d_hid):
        ''' Sinusoid position encoding table '''
        # TODO: make it with torch instead of numpy
		# 位置编码计算函数
        def get_position_angle_vec(position):
            return [position / np.power(10000, 2 * (hid_j // 2) / d_hid) for hid_j in range(d_hid)]
		# 为每个位置计算位置编码的值
        sinusoid_table = np.array([get_position_angle_vec(pos_i) for pos_i in range(n_position)])
        # 获得位置编码
        sinusoid_table[:, 0::2] = np.sin(sinusoid_table[:, 0::2])  # dim 2i
        sinusoid_table[:, 1::2] = np.cos(sinusoid_table[:, 1::2])  # dim 2i+1

        return torch.FloatTensor(sinusoid_table).unsqueeze(0) # 去除第一个维度
    
    def forward(self, x):
        return x + self.pos_table[:, :x.size(1)].clone().detach() # 与词向量相加

缩放点积和多头自注意力

class ScaledDotProductAttention(nn.Module):
    ''' Scaled Dot-Product Attention '''

    def __init__(self, temperature, attn_dropout=0.1):
        super().__init__()
        self.temperature = temperature # 根号d_k,用来放缩
        self.dropout = nn.Dropout(attn_dropout)

    def forward(self, q, k, v, mask=None):

        attn = torch.matmul(q / self.temperature, k.transpose(2, 3))

        if mask is not None:
            attn = attn.masked_fill(mask == 0, -1e9) #让mask中是0的部分变为-1e9

        attn = self.dropout(F.softmax(attn, dim=-1))
        output = torch.matmul(attn, v)

        return output, attn
    
    
class MultiHeadAttention(nn.Module):
    ''' Multi-Head Attention module '''

    def __init__(self, n_head, d_model, d_k, d_v, dropout=0.1): # d_model=512
        super().__init__()

        self.n_head = n_head #头数
        self.d_k = d_k # 维度
        self.d_v = d_v
        
	    # 直接获得所有头的权重矩阵，d_q=d_k
        # 使用全连接层初始化和训练权重矩阵，实际上后续的工作都用一个全连接层生成，然后split
        self.w_qs = nn.Linear(d_model, n_head * d_k, bias=False) 
        self.w_ks = nn.Linear(d_model, n_head * d_k, bias=False)
        self.w_vs = nn.Linear(d_model, n_head * d_v, bias=False)
        self.fc = nn.Linear(n_head * d_v, d_model, bias=False)

        self.attention = ScaledDotProductAttention(temperature=d_k ** 0.5)

        self.dropout = nn.Dropout(dropout)
        self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)

    def forward(self, q, k, v, mask=None):

        d_k, d_v, n_head = self.d_k, self.d_v, self.n_head
        sz_b, len_q, len_k, len_v = q.size(0), q.size(1), k.size(1), v.size(1)

        residual = q # 使用残差连接

        # Pass through the pre-attention projection: b x lq x (n*dv)
        # Separate different heads: b x lq x n x dv
        q = self.w_qs(q).view(sz_b, len_q, n_head, d_k)
        k = self.w_ks(k).view(sz_b, len_k, n_head, d_k)
        v = self.w_vs(v).view(sz_b, len_v, n_head, d_v)

        # Transpose for attention dot product: b x n x lq x dv
        # 将n换到第二个维度，类似于特征图当中的通道
        q, k, v = q.transpose(1, 2), k.transpose(1, 2), v.transpose(1, 2)

        if mask is not None:
            mask = mask.unsqueeze(1)   # For head axis broadcasting.

        q, attn = self.attention(q, k, v, mask=mask)

        # Transpose to move the head dimension back: b x lq x n x dv
        # Combine the last two dimensions to concatenate all the heads together: b x lq x (n*dv)
        q = q.transpose(1, 2).contiguous().view(sz_b, len_q, -1) # 自行百度contiguous()
        q = self.dropout(self.fc(q)) # 相当于上面说的WO
        q += residual

        q = self.layer_norm(q)

        return q, attn

前馈层

class PositionwiseFeedForward(nn.Module):
    ''' A two-feed-forward-layer module '''

    def __init__(self, d_in, d_hid=2048, dropout=0.1):
        super().__init__()
        self.w_1 = nn.Linear(d_in, d_hid) # position-wise
        self.w_2 = nn.Linear(d_hid, d_in) # position-wise
        self.layer_norm = nn.LayerNorm(d_in, eps=1e-6)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):

        residual = x

        x = self.w_2(torch.relu(self.w_1(x)))
        x = self.dropout(x)
        x += residual

        x = self.layer_norm(x)

        return x

编码器和解码器

class EncoderLayer(nn.Module):
    ''' Compose with two layers '''

    def __init__(self, d_model, d_inner, n_head, d_k, d_v, dropout=0.1):
        super(EncoderLayer, self).__init__()
        self.slf_attn = MultiHeadAttention(
            n_head, d_model, d_k, d_v, dropout=dropout) # 多头自注意力
        self.pos_ffn = PositionwiseFeedForward(
            d_model, d_inner, dropout=dropout) # 前馈层

    def forward(self, enc_input, slf_attn_mask=None):
        
        enc_output, enc_slf_attn = self.slf_attn(
            enc_input, enc_input, enc_input, mask=slf_attn_mask) # q attention
        enc_output = self.pos_ffn(enc_output) # 相当对两个输出同时做了softmax,attention已经做过了
        
        return enc_output, enc_slf_attn


class DecoderLayer(nn.Module):
    ''' Compose with three layers '''

    def __init__(self, d_model, d_inner, n_head, d_k, d_v, dropout=0.1):
        super(DecoderLayer, self).__init__()
        self.slf_attn = MultiHeadAttention(
            n_head, d_model, d_k, d_v, dropout=dropout)
        self.enc_attn = MultiHeadAttention(
            n_head, d_model, d_k, d_v, dropout=dropout)
        self.pos_ffn = PositionwiseFeedForward(
            d_model, d_inner, dropout=dropout)

    def forward(self, dec_input, enc_output,slf_attn_mask=None, dec_enc_attn_mask=None):
        # masked-multi-head-attention
        dec_output, dec_slf_attn = self.slf_attn(
            dec_input, dec_input, dec_input, mask=slf_attn_mask) # q,attention
        # encoder-decoder-attention
        # 使用decoder的输出q生成该层的q，encoder的输出q生成该层的k,v
        dec_output, dec_enc_attn = self.enc_attn(
            dec_output, enc_output, enc_output, mask=dec_enc_attn_mask) # mask=none
        dec_output = self.pos_ffn(dec_output)
        
        return dec_output, dec_slf_attn, dec_enc_attn
    

编码块和解码块

class Encoder(nn.Module):
    ''' A encoder model with self attention mechanism. '''

    def __init__(
            self, n_src_vocab, d_word_vec, n_layers, n_head, d_k, d_v,
            d_model, d_inner, pad_idx, dropout=0.1, n_position=200, scale_emb=False):
        '''
        n_src_vocab：词典大小
        d_word_vec：嵌入的维度
 		n_layer：编码块层数
        n——head：头数
        d_k，d_v：k，q和v的维度
        d_model：词向量维度
        d_inner：前馈层中间层维度
        pad_idx：填充长度
        scale_emb：是否进行缩放
        '''

        super().__init__()

        self.src_word_emb = nn.Embedding(
            n_src_vocab, d_word_vec, padding_idx=pad_idx) # 进行嵌入
        
        self.position_enc = PositionalEncoding(
            d_word_vec, n_position=n_position) # 位置嵌入
        
        self.dropout = nn.Dropout(p=dropout)
        
        self.layer_stack = nn.ModuleList([
            EncoderLayer(d_model, d_inner, n_head, d_k, d_v, dropout=dropout)
            for _ in range(n_layers)]) # 定义Encoder stack
        
        self.layer_norm = nn.LayerNorm(d_model, eps=1e-6) # 层归一化
        
        self.scale_emb = scale_emb 
        self.d_model = d_model

    def forward(self, src_seq, src_mask, return_attns=False):

        enc_slf_attn_list = []

        # -- Forward
        enc_output = self.src_word_emb(src_seq) # 词嵌入
        if self.scale_emb:
            enc_output *= self.d_model ** 0.5
        enc_output = self.dropout(self.position_enc(enc_output)) # 位置编码和Drop out
        enc_output = self.layer_norm(enc_output) # 层归一化

        for enc_layer in self.layer_stack:
            enc_output, enc_slf_attn = enc_layer(
                enc_output, slf_attn_mask=src_mask)
            enc_slf_attn_list += [enc_slf_attn] if return_attns else []

        if return_attns:
            return enc_output, enc_slf_attn_list
        return enc_output,


class Decoder(nn.Module):
    ''' A decoder model with self attention mechanism. '''

    def __init__(self, n_trg_vocab, d_word_vec, n_layers, n_head, d_k, d_v,
            d_model, d_inner, pad_idx, n_position=200, dropout=0.1, scale_emb=False):

        super().__init__()

        self.trg_word_emb = nn.Embedding(
            n_trg_vocab, d_word_vec, padding_idx=pad_idx)
        self.position_enc = PositionalEncoding(
            d_word_vec, n_position=n_position)
        self.dropout = nn.Dropout(p=dropout)
        self.layer_stack = nn.ModuleList([
            DecoderLayer(d_model, d_inner, n_head, d_k, d_v, dropout=dropout)
            for _ in range(n_layers)])
        self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)
        self.scale_emb = scale_emb
        self.d_model = d_model

    def forward(self, trg_seq, trg_mask, enc_output, src_mask, return_attns=False):

        dec_slf_attn_list, dec_enc_attn_list = [], []

        # -- Forward
        dec_output = self.trg_word_emb(trg_seq)
        if self.scale_emb:
            dec_output *= self.d_model ** 0.5
        dec_output = self.dropout(self.position_enc(dec_output))
        dec_output = self.layer_norm(dec_output)

        for dec_layer in self.layer_stack:
            dec_output, dec_slf_attn, dec_enc_attn = dec_layer(
                dec_output, enc_output, slf_attn_mask=trg_mask, dec_enc_attn_mask=src_mask)
            dec_slf_attn_list += [dec_slf_attn] if return_attns else []
            dec_enc_attn_list += [dec_enc_attn] if return_attns else []

        if return_attns:
            return dec_output, dec_slf_attn_list, dec_enc_attn_list
        return dec_output,

组建Transformer

class Transformer(nn.Module):
    ''' A sequence to sequence model with attention mechanism. '''

    def __init__(
            self, n_src_vocab, n_trg_vocab, src_pad_idx, trg_pad_idx,
            d_word_vec=512, d_model=512, d_inner=2048,
            n_layers=6, n_head=8, d_k=64, d_v=64, dropout=0.1, n_position=200,
            trg_emb_prj_weight_sharing=True, emb_src_trg_weight_sharing=True,
            scale_emb_or_prj='prj'):

        super().__init__()

        self.src_pad_idx, self.trg_pad_idx = src_pad_idx, trg_pad_idx

        # In section 3.4 of paper "Attention Is All You Need", there is such detail:
        # "In our model, we share the same weight matrix between the two
        # embedding layers and the pre-softmax linear transformation...
        # In the embedding layers, we multiply those weights by \sqrt{d_model}".
        #
        # Options here:
        #   'emb': multiply \sqrt{d_model} to embedding output
        #   'prj': multiply (\sqrt{d_model} ^ -1) to linear projection output
        #   'none': no multiplication

        assert scale_emb_or_prj in ['emb', 'prj', 'none']
        scale_emb = (scale_emb_or_prj ==
                     'emb') if trg_emb_prj_weight_sharing else False
        self.scale_prj = (scale_emb_or_prj ==
                          'prj') if trg_emb_prj_weight_sharing else False
        self.d_model = d_model

        self.encoder = Encoder(
            n_src_vocab=n_src_vocab, n_position=n_position,
            d_word_vec=d_word_vec, d_model=d_model, d_inner=d_inner,
            n_layers=n_layers, n_head=n_head, d_k=d_k, d_v=d_v,
            pad_idx=src_pad_idx, dropout=dropout, scale_emb=scale_emb)

        self.decoder = Decoder(
            n_trg_vocab=n_trg_vocab, n_position=n_position,
            d_word_vec=d_word_vec, d_model=d_model, d_inner=d_inner,
            n_layers=n_layers, n_head=n_head, d_k=d_k, d_v=d_v,
            pad_idx=trg_pad_idx, dropout=dropout, scale_emb=scale_emb)

        self.trg_word_prj = nn.Linear(d_model, n_trg_vocab, bias=False)

        for p in self.parameters(): # 初始化方法
            if p.dim() > 1:
                nn.init.xavier_uniform_(p)

        assert d_model == d_word_vec, \
            'To facilitate the residual connections, \
         the dimensions of all module outputs shall be the same.'

        if trg_emb_prj_weight_sharing:
            # Share the weight between target word embedding & last dense layer
            self.trg_word_prj.weight = self.decoder.trg_word_emb.weight # 共享权重

        if emb_src_trg_weight_sharing:
            self.encoder.src_word_emb.weight = self.decoder.trg_word_emb.weight

    def forward(self, src_seq, trg_seq):

        src_mask = get_pad_mask(src_seq, self.src_pad_idx)
        trg_mask = get_pad_mask(
            trg_seq, self.trg_pad_idx) & get_subsequent_mask(trg_seq)

        enc_output, *_ = self.encoder(src_seq, src_mask) # 只接受第一个
        dec_output, *_ = self.decoder(trg_seq, trg_mask, enc_output, src_mask)
        seq_logit = self.trg_word_prj(dec_output)
        if self.scale_prj:
            seq_logit *= self.d_model ** -0.5

        return seq_logit.view(-1, seq_logit.size(2))
    
    
    
    
def get_pad_mask(seq, pad_idx):
    return (seq != pad_idx).unsqueeze(-2)

def get_subsequent_mask(seq):
    ''' For masking out the subsequent info. '''
    '''会生成一个如下的bool矩阵：
    tensor([[[ True, False, False],
        	 [ True,  True, False],
             [ True,  True,  True]]])
    '''
    sz_b, len_s = seq.size()
    subsequent_mask = (1 - torch.triu(
        torch.ones((1, len_s, len_s), device=seq.device), diagonal=1)).bool()
    # 可以用subsequent_mask = torch.triu(torch.ones((1, len_s, len_s))).transpose(2,1).bool()代替
    return subsequent_mask

附录

Oleksii Kuchaiev and Boris Ginsburg. Factorization tricks for LSTM networks. ↩
Noam Shazeer, Azalia Mirhoseini, Krzysztof Maziarz, Andy Davis, Quoc Le, Geoffrey Hinton,and Jeff Dean. Outrageously large neural networks: The sparsely-gated mixture-of-experts layer. ↩
Łukasz Kaiser and Samy Bengio. Can active memory replace attention? In Advances in Neural Information Processing Systems ↩
Nal Kalchbrenner, Lasse Espeholt, Karen Simonyan, Aaron van den Oord, Alex Graves, and Koray Kavukcuoglu. Neuralmachine translation in linear time ↩
Jonas Gehring, Michael Auli, David Grangier, Denis Yarats, and Yann N. Dauphin. Convolutional sequence to sequence learning ↩

前言​

整体结构​

输入​

Encoder-Decoder​

输出​

注意力机制​

Self-Attention​

缩放点积注意力​

Multi-Head Attention​

位置编码​

为什么需要位置编码？​

正余弦位置编码​

为什么位置编码是有效的？​

更多​

相对距离的方向性​

自注意力对位置编码的影响​

解码块​

Masked Multi-Head Attention​

Endcoder-Decoder Attention​

代码讲解​

位置编码​

缩放点积和多头自注意力​

前馈层​

编码器和解码器​

编码块和解码块​

组建Transformer​

附录​

Footnotes​

前言

整体结构

输入

Encoder-Decoder

输出

注意力机制

Self-Attention

缩放点积注意力

Multi-Head Attention

位置编码

为什么需要位置编码？

正余弦位置编码

为什么位置编码是有效的？

更多

相对距离的方向性

自注意力对位置编码的影响

解码块

Masked Multi-Head Attention

Endcoder-Decoder Attention

代码讲解

位置编码

缩放点积和多头自注意力

前馈层

编码器和解码器

编码块和解码块

组建Transformer

附录

Footnotes