Skip to main content

排序

预备知识​

稳定性：对于任意两个相同关键字的元素，若执行某个排序算法后其相对位置没有发生改变（即本来在前面的元素还在前面），则称该排序算法是稳定的。

内部排序和外部排序：根据数据元素是否完全在内存中，分为内部排序和外部排序两种。

一般情况下内部排序算法都需要通过比较和移动进行排序，但是也有例外，如 基数排序。

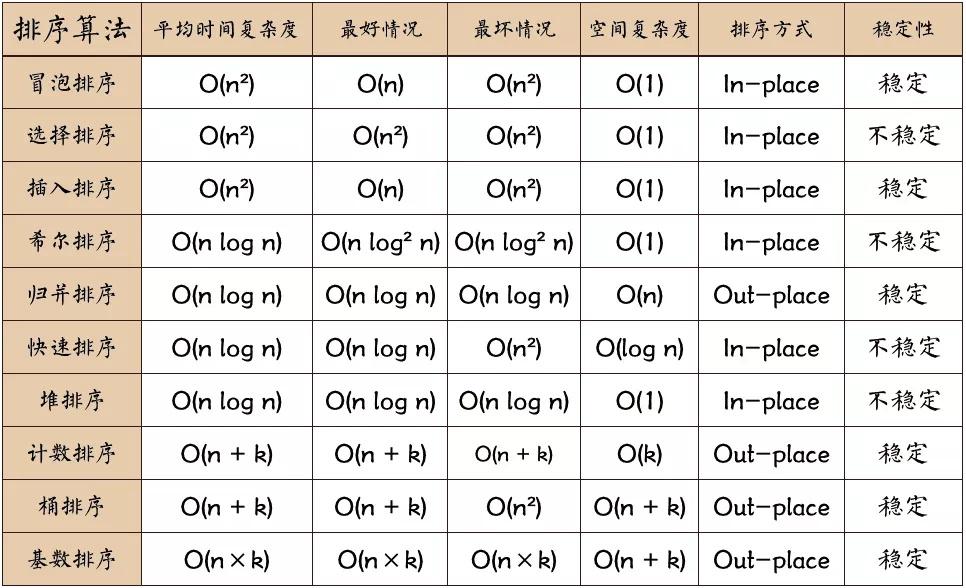
插入排序​

tip

基本思想是将待排序的元素插入到已经排序好的子序列中，可以引申出三种重要的排序算法—— 直接插入排序、折半插入排序 和 希尔排序j.

直接插入排序​

步骤如下：

  1. 初始时将第一个元素作为已经排好的子列；
  2. 对未排好的元素寻找其在已排好子列的位置，同时将所有大于/小于该元素的元素向后排；

代码如下：

void inserSort(int *arr, int len) {
  int i, j, key;
  for (int i = 1; i < len; i++) {
    key = arr[i]; // 使用一个变量存储元素
    j = i - 1;
    while (j >= 0 && arr[j] > key) {
      arr[j + 1] = arr[j]; // 向后移动
      j--;
    }
    arr[j + 1] = key;
  }
}

空间复杂度：O(1)O(1)

时间复杂度：最好的情况只需要从头到尾遍历一次，时间复杂度为 O(n−1)O(n-1)，最坏情况为逆序，总的时间复杂度为 O(n2)O(n^2)，平均情况取 O(n24)O\left( \frac{n^2}{4} \right).

折半插入排序​

由于直接插入排序中已经有一部分元素有序的，因此不再需要遍历寻找，可以使用折半查找，代码如下

void binaryInsertionSort(int *arr, int len) {
  int j, key, left, right;
  for (int i = 1; i < len; i++) {
    key = arr[i];
    left = 0;
    right = i - 1;
    while (left <= right) {
      j = (left + right) / 2;
      if (key < arr[j])
        right = j - 1;
      else // 将相同的元素插入后面，折半插入排序是稳定排序
        left = j + 1;
    }
	// 先移动，再互换
    for (j = i - 1; j >= left; --j)
      arr[j + 1] = arr[j];
    arr[left] = key;
  }
}

减少了比较元素的次数，时间复杂度约为 O(nlog⁡2n)O(n\log_{2}n) ，但是移动元素的次数并没有改变，因此折半插入排序的时间复杂度仍然为 O(n2)O(n^2)；但是对于数据量不大的排序表，往往能表现出很好的性能。

希尔排序​

tip

前两种排序在基本有序和数据不大的情况下性能较好，希尔排序正是基于这两点分析对直接插入排序进行改进而来，又称为 最小增量排序；其基本思想是先将待排序列分割为若干相同长度的子列，这些子列是相隔某个 增量 的元素组成的，对各个子列分别进行直接插入排序，不断减小 增量，使得整个序列基本有序，再对整体进行插入排序（即增量为 11 的情况）。

代码如下，只是在直接插入代码的基础上额外嵌套了一层循环，并将其中的 11 都修改为了 dd ，下面蓝色部分为直接插入排序的代码。

void shellSort(int *arr, int len) {
  int j, key;
  for (int d = len / 2; d >= 1; d /= 2) {
    for (int i = d; i < len; i++) {
      key = arr[i];
      j = i - d;
      while (j >= 0 && arr[j] > key) {
        arr[j + d] = arr[j];
        j -= d;
      }
      arr[j + d] = key;
    }
  }
}

当 nn 在某个特定的范围时，希尔排序的时间复杂度是 O(n1.3)O(n^{1.3})，最坏情况下 （应该还是逆序输入）的时间复杂度是 O(n2)O(n^2)

caution

希尔排序是不稳定的，因为相同的关键字元素可能会被划分到不同的子表中，从而导致了相对次序变化。

交换排序​

tip

交换指的对序列中的两个元素进行交换，常用的算法有冒泡算法和快速排序。

冒泡排序​

tip

冒牌排序这个名称十分形象，指的是每次排序将最小元素（最大元素）放到序列的最后 （或者最前），就像泡泡一样。

代码如下，其中 ii 表示已经排序好子列的索引。

void swap(int *a, int *b) {
  int temp = *a;
  *a = *b;
  *b = temp;
}

void bubbleSort(int *arr, int len) {
  for (int i = 0; i < len - 1; i++) {
    for (int j = len - 1; j > i; j--) {
      if (arr[j - 1] > arr[j]) {
        swap(&arr[j - 1], &arr[j]);
      }
    }
  }
}

冒泡排序可以进一步优化——若在一次遍历当中，没有元素被交换，则说明已经有序了，直接返回即可；代码如下：

void imporvedBubbleSort(int *arr, int len) {
  for (int i = 0; i < len - 1; i++) {
    bool flag = true;
    for (int j = len - 1; j > i; j--) {
      if (arr[j - 1] > arr[j]) {
        swap(&arr[j - 1], &arr[j]);
        flag = false;
      }
    }
    if (flag)
      return;
  }
}

当序列有序时，时间复杂度为 O(n)O(n)，逆序时，每次交换元素需要 33 次移动，比较次数为 n(n−1)2\frac{n(n-1)}{2}，移动次数为 3n(n−1)2\frac{3n(n-1)}{2}，则最坏时间复杂度为 jj.

由于相同时并不会发生交换，则是稳定排序。

快速排序​

tip

快速排序的思想是基于分治，在待排序列中选择一个元素作为基准元素，将所有小于其的元素都放入其左边，大于其的元素都放入其右边，则其最终会被分配到正确的位置上，再通过递归的形式对左右两个部分进行相同的操作，直到所有元素有序。

代码实现上，一般是由头尾两个索引表示区间的长度，基准元素就选择区间中的第一个元素，初始情况，尾索引向头移动，直到遇到某个元素小于基准元素，则将其和基准元素交换；头索引和尾索引的移动是交替的，因为要保证一定有一个索引指向基准元素；当一次划分完成后，基准元素到达了正确的位置，则以其作为分界点，对左右两个部分进行相同的操作即可。

代码如下：

int partition(int *arr, int left, int right) {
  int key = arr[left];
  while (left < right) {
    while (left < right && arr[right] >= key)
      right--;
    arr[left] = arr[right];

    while (left < right && arr[left] <= key)
      left++;
    arr[right] = arr[left];
  }
  arr[left] = key;
  return left;
}

void quickSort(int *arr, int left, int right) {
  if (left < right) {
    int split_index = partition(arr, left, right);
    quickSort(arr, left, split_index - 1);
    quickSort(arr, split_index + 1, right);
  }
}
思考题

如何使用快速排序求出某个序列的第 kk 大的元素？

int topkth(int *arr, int left, int right, int k) {
  if (left < right) {
    int split_index = partition(arr, left, right);
    if (split_index == k)
      return arr[split_index];
    else if (split_index > k)
      return topkth(arr, left, split_index - 1, k);
    else if (split_index < k)
      return topkth(arr, split_index + 1, right, k);
  }
  return -1;
}

空间效率：由于快速排序是递归的，因此需要一个递归工作栈来保存调用信息，其容量和递归调用的最大深度一致。 最好的情况下为 O(log⁡n)O(\log n)，最坏情况下为 O(n)O(n) ，因此平均为 O(log⁡n)O(\log n).

时间效率：与划分是否对称有关，最坏的情况发生在两个区域分别包含 n−1n-1 和 00 个元素，并且发生在每一层上，则时间复杂度为 O(n2)O(n^2).

有许多方式可以提高算法的效率，一种方式是尽量选取一个可以将数据中分的元素，如选取序列头尾和中间三个元素的中间值，或者随机选取。

在最理想的情况下，即 partition 可以做到最平均的划分，速度将大大提升；但是其平均情况下的运行时间和最佳情况很接近，是所有内部排序算法中平均性能最优的算法。

快速排序的非递归实现

大致思路是借助栈来存储每次 partition 之后的结果，并将每次排序的左右坐标存入栈中，再进行排序直到栈为空。

选择排序​

tip

基本思想是每一趟排序在未排的序列中选择一个最小/大的元素，添加到已排序的序列当中。 选择排序包含简单选择排序、堆排序。

简单选择排序​

最简单和纯粹的选择排序思想，每次选择一个最小的交换到已经排好的序列末尾，直到排到倒数第二个元素，这时最后一个元素自然排好

代码如下

void selectSort(int *arr, int len) {
  int min_index;
  for (int i = 0; i < len - 1; i++) {
    min_index = i;
    for (int j = i + 1; j < len; j++)
      if (arr[j] < arr[min_index])
        min_index = j;
    if (min_index != i)
      swap(&arr[i], &arr[min_index]);
  }
}

时间效率：元素移动的次数很少，不会超过 3(n−1)3(n-1) 次，但是比较次数始终是 n(n−1)/2n(n-1)/2 次，因此时间复杂度始终是 O(n2)O(n^2).

稳定性：不稳定，举个例子 [5,8,5,2][5,8,5,2]，第一次交换就会破坏稳定性。

堆排序​

堆是一颗 完全二叉树，即除了最后一层其他所有层都被填满，且最后一层的节点排序为从左至右；根据完全二叉树的性质，对于 1≤i≤[n/2]1\leq i\leq[n/2] ，有

L[i]≥/≤L[2i]L[i]≥/≤L[2i+1]\begin{aligned} &L[i]\geq /\leq L[2i]\\ &L[i]\geq /\leq L[2i+1] \end{aligned}

若最大元素在根节点，则称为大根堆。

构建堆

对于 nn 个元素，可以构建一个完全二叉树（由于根据完全二叉树的性质，可以通过坐标来模拟，因此无需实际建树）；从最后一个节点的父节点开始，其索引为 [n/2][n/2]，比较其孩子的大小，并将其中较大（若是大根堆则是最大的）交换上去，如此遍历直到本层的所有叶节点，在从上一层最右侧的节点进行相同的操作，直到遍历到根节点。

caution

构建完堆之后需要调整从上至下调整一次堆，确保其是 堆。

调整堆

此时 最大值被送到根节点，将其与堆中的最后一个叶节点交换，并从堆中删去该节点，表示其已经排好；由于交换了最大的节点出去，而较小的节点在根的位置，因此需要重新调整堆，将该节点 从上往下 的送下去，即比较根节点的两个孩子，将较大值交换上来，在对交换过去的节点进行同样的操作，直到遍历至叶子节点。

如此循环，直到堆中没有节点。

插入

将节点插入到最后，并从下至上的进行调整。

代码如下

// from top to bottom
void heapify(int *arr, int len, int root_idx) {
  int left = 2 * root_idx + 1, right = 2 * root_idx + 2, largest = root_idx;

  if (left < len && arr[left] > arr[largest])
    largest = left;

  if (right < len && arr[right] > arr[largest])
    largest = right;
  if (largest != root_idx) {
    swap(&arr[largest], &arr[root_idx]);
    heapify(arr, len, largest);
  }
}

void heapSort(int *arr, int len) {
  // from bottom to top
  for (int i = len / 2 - 1; i >= 0; i--)
    heapify(arr, len, i);

  for (int i = len - 1; i >= 0; i--) {
    swap(&arr[i], &arr[0]);
	heapify(arr, i, 0);
  }
}
tip

堆排序适合关键字较多的情况，如从一亿个数中选出前一百个最大值？

使用长度为 100100 的数组，构造小根堆（因为需要求最大值），循环插入剩余的数，若数小于堆顶，则舍弃，若大于则替换，并重新调整堆，直到遍历完所以数字。

时间效率：构建堆的时间复杂度为 O(n)O(n) ，之后有 n−1n-1 次向下调整的操作，每次的时间复杂度是 O(h)O(h)，故最好、最坏和平均情况下，堆排序的时间复杂度都是 O(nlog⁡2n)O(n\log_{2}n) .

稳定性：不稳定，如序列 [1,2,2][1,2,2]，构造堆时可能将第一个二交换至堆顶，而最终排序结果其显然是在最后的位置。

归并排序​

tip

归并排序的思想和上述基于选择和交换的排序都不相同，归并 表示将两个或以上的有序序列合并为一个新的有序序列，初始情况下每个有序序列的长度为 11，不断的两两归并直到包含真整个序列，该方法称为二路归并排序。

代码如下，高亮部分的代码仅会执行一个，表示将剩下的元素全部添加过去。

void merge(int *arr, int left, int middle, int right, int *tmp_arr) {
  // left arr: left - middle        right arr: middle + 1 - right
  // both of them are sorted.
  int i, j, k;
  for (i = left; i <= right; i++)
    tmp_arr[i] = arr[i];

  for (i = left, j = middle + 1, k = left; i <= middle && j <= right; k++) {
    if (tmp_arr[i] < tmp_arr[j])
      arr[k] = tmp_arr[i++];
    else
      arr[k] = tmp_arr[j++];
  }

  // for remainder, only one while will be executed.
  while (i <= middle)
    arr[k++] = tmp_arr[i++];
  while (j <= right)
    arr[k++] = tmp_arr[j++];
}

void mergeSort(int *arr, int left, int right, int *tmp_arr) {
  if (left < right) {
    int middle = (left + right) / 2;
    mergeSort(arr, left, middle, tmp_arr);
    mergeSort(arr, middle + 1, right, tmp_arr);
    merge(arr, left, middle, right, tmp_arr);
  }
}

调用代码时需要创建一个 tmp_arr 辅助数组，记得结束时释放。

空间效率：不难发现，空间复杂度为 O(n)O(n).

时间效率：每趟归并的时间复杂度为 O(n)O(n)，进行 log⁡2n\log_{2}n 次归并，因此总的时间复杂度为 O(nlog⁡2n)O(n\log_{2}n).

稳定性：归并操作不改变相同元素的相对位置，因此是稳定的。

info

对于 kk 路归并排序而言，归并的次数是 [log⁡kn][\log_kn]，时间复杂度还是 nlog⁡2nn\log_{2}n.

基数排序​

tip

同样是不基于比较和移动，而是基于关键字各位的大小进行排序，以关键字是数字为例，可以从低位到高位将关键字不断的分为几个集合，再按照基数顺序排回，直到排完最高位，此时排序完成。

代码如下，第一处高亮表示将各个基数的计数转换为对应基数的值应该在辅助数组中的位置，第二处高亮要注意应该从数组的后面往前面排序，因为每次放入一个数后，对应基数的 count index 会减一，如果从头开始则会覆盖之前的数据。

int getMax(int *arr, int n) {
  int max = arr[0];
  for (int i = 1; i < n; i++) {
    if (arr[i] > max) {
      max = arr[i];
    }
  }
  return max;
}

void countSort(int *arr, int n, int exp) {
  int output[n], counts[10] = {0};

  for (int i = 0; i < n; i++)
    counts[(arr[i] / exp) % 10]++;

  // convert count to index
  for (int i = 1; i < 10; i++)
    counts[i] += counts[i - 1];

  for (int i = n - 1; i >= 0; i--) {
    output[counts[(arr[i] / exp) % 10] - 1] = arr[i];
    counts[(arr[i] / exp) % 10]--;
  }

  for (int i = 0; i < n; i++)
    arr[i] = output[i];
}

void radixSort(int *arr, int n) {
  int max = getMax(arr, n);
  for (int exp = 1; max / exp > 0; exp *= 10)
    countSort(arr, n, exp);
}

通用的实现是使用队列，将属于同一基数的数放在同一个队列。

空间效率：显然是 O(n+r)O(n+r)，其中 rr 为基数的个数。

时间效率：基数排序的次数和数据的位数 dd 有关，一次分配需要 O(n)O(n) ，则其时间复杂度为 O(d(n+r))O(d(n+r))，与序列的初始状态无关。

稳定性：稳定。

外部排序​

tip

外部排序指的是待排序文件较大，内存一次放不下，需要放在外存的文件排序，为了平衡归并中 I/OI/O 次数，通常使用 增大归并路数和减少归并段个数 的方式，前者可使用 败者树，后者使用 置换 - 选择排序 来增大归并段长度并减少其个数，最后由长度不等的归并段，进行 多路平衡归并，这需要构造最佳归并树。

外部排序通常使用 归并排序，包括两个阶段：

  1. 根据内存缓冲区的大小，将外存上的文件分成若干个长度为 ll 的子文件，依次读入内存进行内部排序，再写回硬盘；这些有序的子文件被称为 归并段 或者 顺串；
  2. 使用归并排序的方式对这些归并段进行连续归并，直到所有文件有序。
tip

归并时由于归并段已经有序，而内存中最多只能容纳一个归并段，因此可以使用多个 输入缓冲区 和 输出缓冲区 解决这个问题，当输出缓冲区满之后，直接写入文件即可。

由于外存的读写是以块为单位的，因此每次归并都需要一定的读写，但是可以通过增加归并路数，或者增加初始归并段长度（但是受限于内存，往往是行不通的）来减少归并次数，从而降低 I/OI/O 次数；对于 rr 个初始归并段，若使用 kk 路平衡归并，归并树可以使用 严格 k 叉树，第一躺可以将其归并为 [r/k][r/k] 个归并段，总的归并躺数为 [log⁡kr]=h−1[\log_{k}r]=h-1，其中 hh 为树高。

严格 k 叉树

只有度为 kk 和 00 的节点的 kk 叉树，哈夫曼树就是一个严格 kk 叉树。

多路平衡归并与败者树​

增加归并路数时，内部归并的时间将增加，需要在 kk 个关键字中选择最小的，因此需要进行 k−1k-1 次比较，每趟归并 nn 个元素就需要 (n−1)(k−1)(n-1)(k-1) 次比较，则 SS 趟归并的比较总次数为

S(n−1)(k−1)=[log⁡kr](n−1)(k−1)=[log⁡2r](n−1)(k−1)[log⁡2k]S(n-1)(k-1)=[\log_{k}r](n-1)(k-1)=\frac{[\log_{2}r](n-1)(k-1)}{[\log_{2}k]}

其中 k−1log⁡2k\frac{k-1}{\log_{2}k} 会随 kk 增长而增长，因此使用普通的内部归并会降低减少外存访问的收益，因此引入了败者树，其是树形选择的一种变体，可以视为一颗完全二叉树。 kk 个叶节点中分别存放 kk 个归并段在归并过程中当前参与比较的记录，内部节点用于记录左右子树中的失败者，而让胜者继续向上比较直到根节点，比较两个数时，大的为失败者，小的为胜利者，则根节点指向的数为最小数。

败者树的树深度为 [log⁡2k][\log_{2}k]，因此 kk 个记录中选择最小关键字，最多需要 [log⁡2k][\log_{2}k] 次比较，因此使用败者树之后总的比较次数为

S(n−1)[log⁡2k]=(n−1)[log⁡2r]S(n-1)[\log_{2}k]=(n-1)[\log_{2}r]
caution

归并路数并不是越大越好，太大就需要增加太多输入缓冲区的个数，若可供使用的内存空间不变，就需要减少每个输入缓冲区的大小，使用内存与外存交换数据的次数增加。

置换 - 选择排序（生成初始归并段）​

大致方式如下：

  1. 先从输入文件中输入 ww 个记录到工作区中；
  2. 从工作区中挑选一个最小的，记作 MINIMAXMINIMAX，同时输出到目标文件中；
  3. 若输入文件非空，则继续输入下一个记录到工作区；
  4. 再从工作区中挑出一个 最小的大于 MINIMAX 的数，记为新的 MINIMAXMINIMAX ，同时输出到目标文件中；
  5. 重复 3-5，知道在工作区总挑选不出新的 MINIMAXMINIMAX 为止，由此得到一个初始归并段；
  6. 重复 2-6，直到工作区为空，由此得到全部初始归并段。

最佳归并树​

经过选择 - 置换排序后得到的初始归并树长度互不相同，不同的归并顺序也会导致 I/OI/O 次数不同，因此需要让短的归并段先归并，使用归并树表示就是其带权路径，权值就是对应的归并段长度，实际上可以使用 kk 叉哈夫曼树得到最少的 I/OI/O 次数，也被称为最优归并树。

显然不是所有的数量的归并段都能使用一个严格 kk 叉树表示，因此需要添加一定的虚段（权值为 00），而严格 kk 路哈夫曼树的节点个数应该满足

n0=(k−1)nk+1  ⟹  n0−1=(k−1)n_{0}=(k-1)n_{k}+1\implies n_{0}-1=(k-1)

由于归并段所在的节点全是叶子节点即 n0n_{0}，因此通过 (n0−1)%(k−1)(n_{0}-1)\%(k-1) ，若结果为 00，则说明可以构成最佳归并树，若等于 μ\mu，则需要添加 k−μ−1k-\mu-1 个虚段。